The Wedge Product | Daymares & Equations

The wedge product can be thought of as what the vector product $\mathbf{a \times b}$ of vector analysis should have been. If $\mathbf{i}, \mathbf{j}, \mathbf{k}$ are the unit vectors along the three coordinate axes in 3-dimensional euclidean space and

$\begin{align*} a & = \lambda_1 \mathbf{i} + \lambda_2 \mathbf{j} + \lambda_3 \mathbf{k}, \\ b & = \xi_1 \mathbf{i} + \xi_2 \mathbf{j} + \xi_3 \mathbf{k} \end{align*}$

are two vectors, then the calculus student is told that

$a \times b \; = \; \det \left( \begin{matrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ \lambda_1 & \lambda_2 & \lambda_3 \\ \xi_1 & \xi_2 & \xi_3 \end{matrix} \right) .$

This result, $a \times b$ , is a vector perpendicular to both $a$ and $b$ and oriented according to the “right-hand rule.”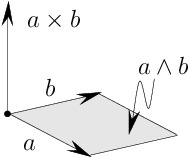

Unfortunately for people who want to do more complicated things (for example, relativity theorists working in 4-dimensional space-time), the vector product only works — is indeed only defined — in three dimensions.

But the wedge product of vectors, $a \wedge b$ , works in any dimension, and the vector product, $a \times b$ , can be thought of, in a certain sense, as a special case or modification of $a \wedge b$ . The trick is that if you form the wedge product $a \wedge b$ of vectors $a, b$ in the $n$ -dimensional euclidean space $\mathbb{R}^n$ , the result is not a vector in $\mathbb{R}^n$ but rather a “vector” in a different vector space $\Lambda^2 \mathbb{R}^n$ .

To gain some feeling as to what this new “vector” is, recall that a vector $a$ in the plane or in 3-dimensional space is often thought of as a directed line segment. If $a$ and $b$ are vectors in $\mathbb{R}^n$ , then they determine a parallelogram having $a$ and $b$ as its sides. We then identify $a \wedge b$ with this parallelogram. More precisely, we identify it with an equivalence class of such parallelograms, and we also equip these parallelograms with a sort of “right-handedness” or “left-handedness,” what a mathematician likes to call an orientation.

The process can be extended. We can form “simple 3-vectors” $a \wedge b \wedge c$ which we can think of as “oriented” 3-dimensional parallelepipeds and then go on to even higher-dimensional “simple $k$ -vectors” $a_1 \wedge \cdots \wedge a_k$ . We can multiply them by scalars and add them and use them to do analytic geometry and calculus on curved surfaces in $n$ -dimensional euclidean space.

The reader who wants to know more is invited to click on The Wedge Product and Analytic Geometry and download a pdf file of the article which appeared in the August-September, 2008, issue of The American Mathematical Monthly. This article, written by Mehrdad Khosravi and yours-truly, presumably has at least a modicum of value since it won a Lester R. Ford Award for exposition.